EJERCICIOS DE RESTA

APRENDIENDO A RESTAR

UNIDADES Y DECENAS FORMACIÓN

Ejercicios de matemáticas resta

Para iniciar al niño en la ejecución de restas. Ejercicios para que los niños de 5 años aprendan a restar. Operaciones matemáticas de restas.

Estas fichas están realizadas por profesores de infantil y primaria para ayudar a los niños en casa con los conocimientos que aprenden en el colegio. Con este ejercicio los niños podrán iniciarse en la realización de restas y practicarán las restas

 

Ficha de matemáticas

• Tiempo de realización: 30 minutos
• Dificultad: Media
• Pdf: Aprender a restar

Objetivos de la ficha

• Realizar restas sencillas con apoyo gráfico
• Iniciación a las restas
• Autoevaluar el resultado de la actividad

Materiales necesarios

- Página impresa de la actividad.
- Lápiz. 

Sugerencias para realizar la actividad de la ficha

1. Indique al niño que observe la ficha y pregúntele que ve en ella.
2. Léale al niño el enunciado de la actividad.
3. Hágale preguntas sobre lo que hay en la ficha. Háblele del signo de la resta. Realice restas sencillas con diferentes objetos cercanos al niño.
4. Tras realizar la ficha, pídale al niño que coloree la carita de acuerdo a cómo crea
que lo ha hecho.

La resta o sustracción

La sustracción es una de las operaciones aritméticas junto con la suma, la multiplicación y la división y a partir de la cual es plausible obtener la diferencia que existe en dos cantidades propuestas. Asimismo, la conocemos popularmente como resta y se la simboliza a partir del signo -.

El procedimiento a partir del cual es plausible obtener esa mencionada diferencia consiste en presentar determinada cantidad, por ejemplo 9, se elimina una parte de la misma, como ser 3, y entonces el resultado de esa eliminación que en este caso sería 6, es el resto, en tanto, las denominaciones del primer número y del segundo son minuendo y sustraendo, respectivamente.

Así como sucede en la operación de la suma o adición, al minuendo se lo ubicará por sobre el sustraendo, organizando las cifras en cuestión en columnas, que van de la derecha a la izquierda y ordenadas en función de unidades, decenas, centenas y millares.

Es importante tener en consideración algunas cuestiones que influyen en el resultado de la sustracción como ser: en el caso que la cifra del minuendo sea menor respecto del sustraendo deberán sumarse diez unidades; si el minuendo es cero será considerado como un diez, en cambio si el 0 está en el lugar del sustraendo no hay modificación alguna.

Es posible realizar la comprobación del resultado de esta operación sumando el resultado obtenido con el sustraendo. Si se confirma el minuendo, entonces, estará correctamente hecha la operación.

Cabe destacar que la operación inversa a la sustracción es la suma o adición, en la cual por supuesto se efectúa la acción contraria añadir o agregar cantidades para conocer cuál es el resultado de la suma de las mismas.

Resta de números naturales hasta el 19

REPASO UNIDADES Y DECENAS

SUMAS HASTA EL 19 EJERCICIOS

Suma de números naturales hasta el 19

UNIDADES Y DECENAS

REPASO DE UNIDADES Y DECENAS

ACTIVIDADES DECENAS Y UNIDADES

UNIDADES, DECENAS, CENTENAS

Cuando escribimos un número, la primera cifra por la derecha representa las unidades, la segunda por la derecha las decenas y la tercera por la derecha las centenas.

Veamos el número 125:

La relación entre ellas es:

1 decena = 10 unidades
1 centena = 100 unidades
1 centena = 10 decenas

El número anterior 125 se puede descomponer entonces:

1 centenas = 100 unidades
2 decenas = 20 unidades
5 unidades = 5 unidades

Podemos comprobar que si sumamos estos tres componentes:

100 + 20 + 5 = 125

Cuando sumamos o restamos números hay que escribirlos de forma que:

Todas las unidades estén en la columna de las unidades.
Todas las decenas estén en la columna de las decenas.
Todas las centenas estén en la columna de las centenas.

Veamos la siguiente suma: 145 + 56 + 678

Vamos a ver ahora una resta: 361 - 72

Unidades, decenas y centenas

Unidades, decenas y centenas

Las unidades

La unidad es el elemento entero más pequeño que podemos contar. Vamos a representar una unidad con un cubito:

Para abreviar la palabra “unidad”, escribiremos “u”, por ejemplo:

Las decenas

Veamos un número de unidades un poco más grande:

Hay muchas unidades, ¿verdad? ¡Pues imagínate cuántas habrá si representamos un número mayor!

Por eso, utilizamos la decena, que agrupa de 10 en 10 las unidades:

Vamos a representar el número 18 utilizando la decena. Debes saber que abreviamos “decena” con la letra “d”. Así:

La decena es un valor más grande que la unidad, ya que en una decena hay 10 unidades. Mira otros ejemplos:

Las centenas

Pero nos pasa lo mismo cuando llegamos al 100. Por ejemplo, mira cómo se representaría con decenas y unidades el número 101:

Por eso utilizamos la centena, que equivale a 10 decenas o, lo que es lo mismo, 100 unidades:

Abreviamos “centena” con la letra “c”. Vamos a ver dos ejemplos:

Valor posicional

Ahora que ya conocemos las unidades, decenas y centenas, vamos a ver el valor posicionalde los números.

Vamos a situar todos los números que hemos visto en una tabla, siguiendo estas instrucciones:

• En la columna de la izquierda, escribiremos el número completo.
• En las tres siguientes columnas, en las que pone “c”, “d” y “u”, tenemos que colocar el número, escribiendo una sola cifra en cada hueco, siempre el último número en las unidades:
• En la última columna, expresamos el número descompuesto en centenas, decenas y unidades.

NÚMEROS HASTA EL 19

Escribir y leer los números hasta el 19

Aprende los Números

El origen de los números es muy antiguo y surgió por la necesidad que tenía el hombre de contar. El llegar a escribir los números como ahora lo hacemos no fue nada fácil. En un principio contaban con los dedos, con piedras, haciendo marcas en palos o nudos en una cuerda.

Los sistemas de numeración de las civilizaciones antiguas representaban bien los números pequeños, pero les era muy difícil hacerlo con las grandes cantidades porque tenían que poner tantos símbolos que era muy poco práctico.

Sistemas De Numeración
Egipcio	Babilónico
Griego	Chino

El sistema que nosotros empleamos, Sistema Decimal, fue inventado por los indios y traído a Europa por los árabes. Su gran éxito consistió en introducir el símbolo del cero, que permite con sólo diez símbolos, representar cualquier número por grande que sea.

SUMA EN LA SEMIRRECTA NUMÉRICA EJERCICIOS

Practico ejercicios en la semirrecta

PRACTICAR Y REPASAR EJERCICIOS EN LA SEMIRRECTA

semirrecta

También llamado media línea. Es una línea recta que se extiende desde un punto.Conjunto que consiste en un punto P sobre una línea recta y todos los puntos de la línea a un lado de P.El punto P es el punto inicial, u origen, de la semirrecta. A una semirrecta se le puede llamar media línea cerrada ya que incluye el punto inicial P. Una media línea abierta no incluye el punto inicial P.

Resolver problemas de la suma en la semirrecta

Suma hasta el 9 en la semirrecta numérica

Sumas en la semirrecta hasta el 9

RESTA Y SUMA EN LA SEMIRRECTA NUMÉRICA REPASO

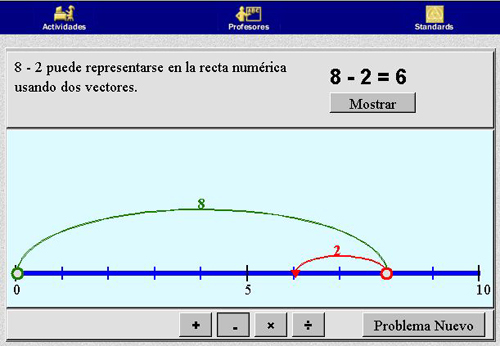
RESTA EN LA SEMIRRECTA EJERCICIOS

La resta o sustracción es una de las cuatro operaciones básicas de la aritmética; se trata de una operación de descomposición que consiste en, dada cierta cantidad, eliminar una parte de ella, y el resultado se conoce como diferencia o resto.

Es la operación inversa a la suma. Por ejemplo, si a+b = c, entonces c–b = a.

En la resta, el primer número se denomina minuendo y el segundo es el sustraendo. El resultado de la resta se denomina diferencia.

En el conjunto de los números naturales, N, sólo se pueden restar dos números si el minuendo es mayor que el sustraendo. De lo contrario, la diferencia sería un número negativo, que por definición estaría excluido del conjunto. Esto implica la ampliación del conjunto de los números naturales con un nuevo concepto de número, el conjunto de los números enteros Z, que incluye a los naturales. Esto también es así para otros conjuntos con ciertas restricciones, como los números reales positivos.

En matemáticas avanzadas no se habla de «restar» sino de «sumar el opuesto». En otras palabras, no se tiene a – b sino a + (–b), donde –b es el elemento opuesto de b respecto de la suma.

Resta en la semirrecta numérica

RESTA EN LA SEMIRRECTA NUMÉRICA CON NÚMEROS NATURALES HASTA EL 5

LA RESTA O SUSTRACCIÓN

La resta o sustracción es una de las cuatro operaciones básicas de la aritmética;se trata de una operación de descomposición que consiste en, dada cierta cantidad, eliminar una parte de ella, y el resultado se conoce como diferencia o resto.

Resta de números naturales hasta el 5

   

ejercicios de la semirecta

SEMIRRECTA

Semirrecta

Haz de rayos.

Se le llama semirrecta, a cada una de las dos partes en que queda dividida una recta al ser cortada en cualquiera de sus puntos. Es la parte de una recta conformada por todos los puntos que se ubican hacia un lado de un punto fijo de la recta, denominado origen, a partir del cual se extiende indefinidamente en una sola dirección.

Semirrecta opuesta

La semirrecta opuesta de una semirrecta es la otra semirrecta salida de la recta que define la primera.

Cada semirrecta solo tiene una semirrecta opuesta.

• Una semirrecta y su semirrecta opuesta tienen el mismo origen.

SEMIRRECTA NUMÉRICA

Suma en la semirrecta numérica

Resuelve adiciones sin reagrupación con números   de una

cifra en la semirrecta numérica.